Rational Approximations for the Modified Bessel Function of the Second Kind – K0(x) for Computations with Double Precision

This is the third post in a series of studies on minimax rational approximations used for computation of modified Bessel functions. Previous posts are: I₀(x) and I₁(x).

Today we will consider modified Bessel function of the second kind – $K_0(x)$ . As usual, at first we check properties of each method and then propose our original approximations which deliver better accuracy.

BesselK Functions (1st Kind, n=0,1,2,3)

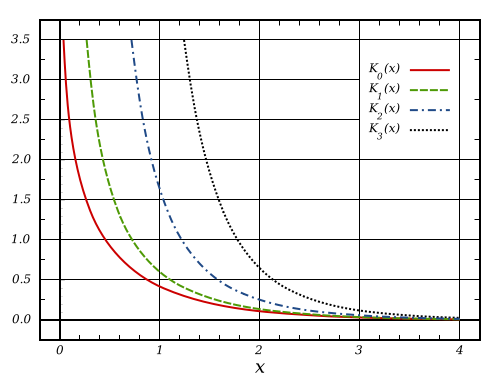
Blair & Russon^[1] proposed following rational approximations for small arguments, $x<1$ :

(1) $\begin{alignat*}{2} K_0(x)+\ln(x)I_0(x)&\approx P_n(x^2)/Q_m(x^2)\\ I_0(x)&\approx P_r(x^2)/Q_s(x^2), \end{alignat*}$

For large values of $x$ different function is used:

(2) $\begin{equation*} x^{1/2}e^x K_0(x) \approx P_v(1/x)/Q_u(1/x) \end{equation*}$

All software libraries relying on rational approximations for computing $K_0(x)$ use (1) and (2) with small variations in coefficients of polynomials $P_*(x)$ and $Q_*(x)$ .

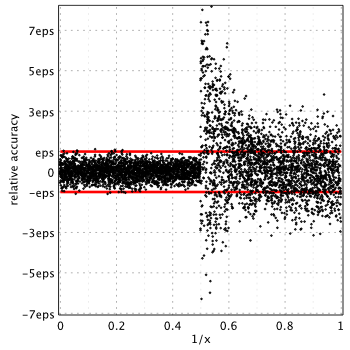
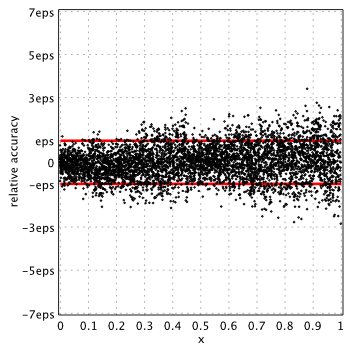
Accuracy analysis for the widely used approximation/libraries are below. Relative error is measured in terms of machine epsilon ( eps = 2^-52 ˜ 2.22e-16) against “true” values of the function computed in quadruple precision by Maple.

Red lines show natural limits for relative error we expect for double precision computations.

Blair & Russon^[1] and Boost 1.59.0^[2]

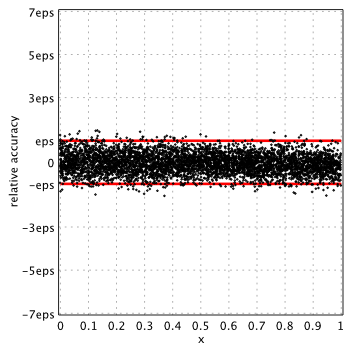
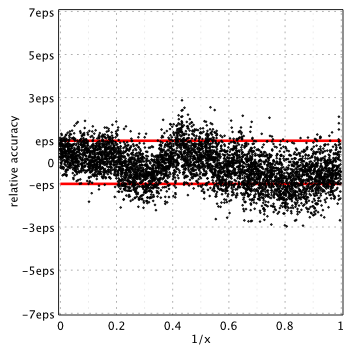
Boost uses coefficients from tables 29 (p.19), 72 (p.28) and 115 (p.39) of original report^[1].

SPECFUN 2.5^[3]

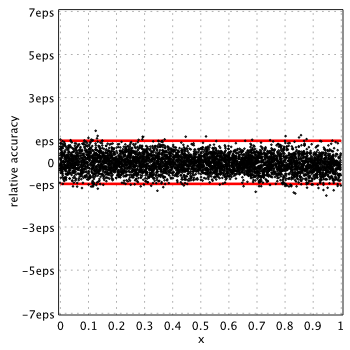
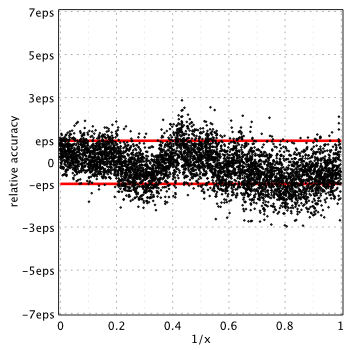
SPECFUN uses improved form of approximation for $x<1$ (see (3) below) and original Blair & Russon coefficients for larger arguments (same as Boost).

Numerical Recipes, 3rd edition, 2007^[4]

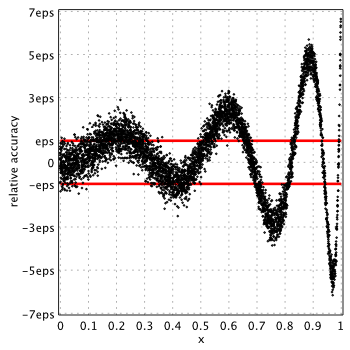
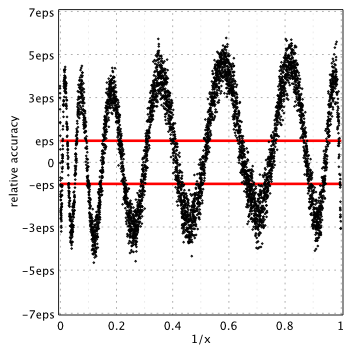
Authors of Numerical Recipes propose their own coefficients (unfortunately with reduced accuracy).

GNU GSL 2.0^[5]
(GSL uses Chebyshev series)

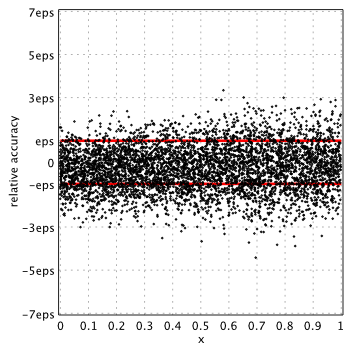
MATLAB 2015a^[6]
(MATLAB uses Chebyshev series)

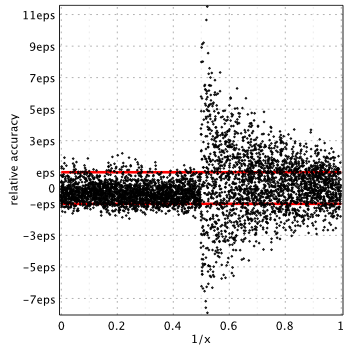
Surprisingly MATLAB provides the lowest accuracy for $x\in[0,2]$ compared to all other libraries. Relative error is up to 11.48eps near the $x=2$ . GSL and MATLAB use Chebyshev expansion for computations and apparently both suffer from similar issues.

After investigating the source code of GSL, we believe the reason for such behavior is that Chebyshev coefficients are stored in reduced accuracy with incorrectly rounded last several digit(s). In fact, GSL has the same issue in all modified Bessel functions (and probably others)! Avoid using the built-in MATLAB besselk and GSL if you need high accuracy results.

Peak relative error^† in terms of machine epsilon – $K_0$
Method/Software	$x\in[0,1)$	$x \in[1,\infty)$
Minimax Rational Approximations:
Blair & Russon / Boost 1.59.0	2.0	3.65
Numerical Recipes, 2007	7.4	6.42
SPECFUN 2.5	1.6	3.65
Refined – (4), (5)	1.6	2.18
Chebyshev Expansions:
GNU GSL 2.0	4.44	9.29
MATLAB 2015a	3.78	11.48

†computed over 50K uniformly distributed random samples in each interval

Refined Approximations

In order to improve the accuracy we switch to different approximation formula for $I_0(x)$ near zero:

(3) $\begin{alignat*}{2} K_0(x)+\ln(x)I_0(x)&\approx P_n(x^2)/Q_m(x^2)\\ I_0(x)&\approx [x/2]^2 P_r([x/2]^2)/Q_s([x/2]^2)+1, \end{alignat*}$

This form reflects behavior of $I_0(x)$ for small arguments well and showed good results in our previous study. Interestingly that SPECFUN is also using this form, but only for computing the $K_0(x)$ .

We use the same formula for large arguments as in (2).

To find optimal approximations we run brute force search among all minimax rational approximations with $n+m\le30$ . The search criteria includes not only minimization of theoretical approximation error but also minimization of actual relative error in double precision. Please see our other posts for more information: I₀(x) and I₁(x).

Search revealed approximations with following properties:

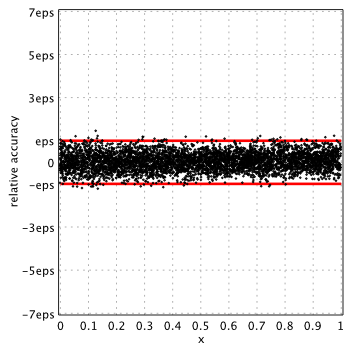
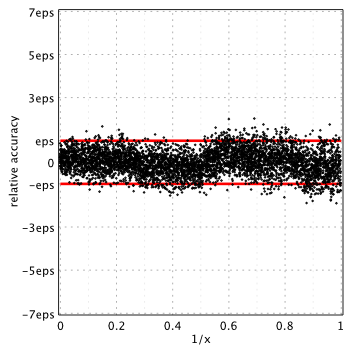
Maximum error is 1.6eps for small arguments and 2.18eps for $x\ge1$ .

Final expressions for optimal approximations:

For small arguments, $x<1$ :

(4) $\begin{alignat*}{2} K_0(x)+\ln(x)I_0(x)&\approx P_7(x^2)\\ I_0(x)&\approx [x/2]^2P_6([x/2]^2)+1, \end{alignat*}$
For large arguments, $x\ge1$ :

(5) $\begin{equation*} x^{1/2}e^x K_0(x) \approx P_{21}(x^{-1})/Q_2(x^{-1}) \end{equation*}$

Coefficients of the polynomials:

n	$P_{7}(x)$
0	1.1593151565841244842077226e-01
1	2.7898287891460317300886539e-01
2	2.5248929932161220559969776e-02
3	8.4603509072136578707676406e-04
4	1.4914719243067801775856150e-05
5	1.6271068931224552553548933e-07
6	1.2082660336282566759313543e-09
7	6.6117104672254184399933971e-12

n	$P_{6}(x)$
0	1.0000000000000000044974165e+00
1	2.4999999999999822316775454e-01
2	2.7777777777892149148858521e-02
3	1.7361111083544590676709592e-03
4	6.9444476047072424198677755e-05
5	1.9288265756466775034067979e-06
6	3.9908220583262192851839992e-08

n	$P_{21}(x)$
0	1.0694678222191263215918328e-01
1	9.0753360415683846760792445e-01
2	1.7215172959695072045669045e+00
3	-1.7172089076875257095489749e-01
4	7.3154750356991229825958019e-02
5	-5.4975286232097852780866385e-02
6	5.7217703802970844746230694e-02
7	-7.2884177844363453190380429e-02
8	1.0443967655783544973080767e-01
9	-1.5741597553317349976818516e-01
10	2.3582486699296814538802637e-01
11	-3.3484166783257765115562496e-01
12	4.3328524890855568555069622e-01
13	-4.9470375304462431447923425e-01
14	4.8474122247422388055091847e-01
15	-3.9725799556374477699937953e-01
16	2.6507653322930767914034592e-01
17	-1.3951265948137254924254912e-01
18	5.5500667358490463548729700e-02
19	-1.5636955694760495736676521e-02
20	2.7741514506299244078981715e-03
21	-2.3261089001545715929104236e-04

n	$Q_{2}(x)$
0	8.5331186362410449871043129e-02
1	7.3477344946182065340442326e-01
2	1.4594189037511445958046540e+00

text

Conclusion

Proposed new minimax rational approximations for computation of modified Bessel function of the second kind – $K_0(x)$ deliver the smallest relative error among commonly used approximations of the same type (especially for large arguments). Notably, even optimal approximations are not able to produce error under machine epsilon. This is because limited capabilities of rational approximations. Higher accuracy needs polynomials of higher degree, which prone to become ill-conditioned. Proposed approximations provide balance between accuracy and ill-conditioning.

Acknowledgements

I would like to thank Anne Russon who helped me to get access to the report^[1] – as it is not available on Internet and Anne helped to get the copy from archive of Canadian Nuclear Laboratories. Thank you Eleanor Miller and Tanya Martin!

Please provide link to this page if you use the approximations in your work.

References

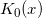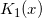Russon A.E., Blair J.M., Rational function minimax approximations for the modified Bessel functions $K_0(x)$ and $K_1(x)$ , AECL-3461, Chalk River Nuclear Laboratories, Chalk River, Ontario, October 1969.
Boost – free peer-reviewed portable C++ source libraries. Version 1.59.0. Boost: Modified Bessel function of the second kind.
Cody W.J., Algorithm 715: SPECFUN – A Portable FORTRAN Package of Special Function Routines and Test Drivers, ACM Transactions on Mathematical Software, Volume 19, Number 1, March 1993, pages 22-32. SPECFUN: Modified Bessel function of the second kind.
Press, William H. and Teukolsky, Saul A. and Vetterling, William T. and Flannery, Brian P. Numerical Recipes 3rd Edition: The Art of Scientific Computing, 2007, Cambridge University Press, New York, USA.
M. Galassi et al, GNU Scientific Library Reference Manual, 3rd Edition (January 2009), ISBN 0954612078.
MATLAB 2015a, The MathWorks, Inc., Natick, Massachusetts, United States.

Rational Approximations for the Modified Bessel Function of the Second Kind – `K₀(x)` for Computations with Double Precision

Refined Approximations

Conclusion

Acknowledgements

References

Latest Updates

March 27, 2024

February 29, 2024

January 5, 2024

November 29, 2023

Being Used At: