Version 3.9.0 Release Notes

by Pavel Holoborodko on November 20, 2015

Over the course of the last three months we have added many important improvements and bug fixes into toolbox. We decided to produce the new official release as it contains critical updates for all platforms (even though eigensolver for large sparse matrices is not included yet).

Here is the main changes:

  1. The Core: Multithreading manager has been updated with better load-balancing and non-blocking synchronization. This results in 15-20% performance boost in all operations with dense matrices, even including the matrix multiplication.
  2. Eigenvalues.
    • Speed of unsymmetric generalized eigen-decomposition has been improved. Now toolbox uses blocked version of Hessenberg tridiagonal reduction[1] which gives us timings lower by 20%.
    • Speed of symmetric eigen-decomposition has been boosted up as well. All cases are covered, including the standard and generalized problems in quadruple and arbitrary precision modes and both complexities.


      Actual speed-up factor depends on number of cores and matrix size. In our environment Core i7/R2015a/Win7 x64 we see x3 times ratio for 1Kx1K matrix:

      mp.Digits(34)
A = mp(rand(1000)-0.5);
A = A+A';
 
% Previous versions
tic; eig(A); toc;
Elapsed time is 48.154 seconds.
 
% 3.9.0.9919
tic; eig(A); toc;      % x3.4 times faster
Elapsed time is 14.212 seconds.

      Speed-up is even higher for other precision levels:

      mp.Digits(50)
A = mp(rand(1000)-0.5);
A = A+A';
 
% Previous versions
tic; eig(A); toc;
Elapsed time is 204.431 seconds.
 
% 3.9.0.9919
tic; eig(A); toc;      % x5.3 times faster
Elapsed time is 38.534 seconds.

      In fact, all operations with dense symmetric/Hermitian and SPD/HPD matrices have became faster: chol, inv, det, solvers, etc. For example, speed-up ratio for inv is up to x10 times depending on matrix structure and number of cores.

  3. Basic matrix routines: det, cond, trace, rank, inv and norm have been re-written for performance and better compatibility with MATLAB. For example, now dense solver (\) computes rcond, inv has better support for inf-values, det handles singular matrices well, etc.
    A = magic(5);
A(3,:) = A(2,:)+10*eps;   % make problem ill-conditioned in double precision
b = rand(5,1);
 
x = A\b;
'Warning: Matrix is close to singular or badly scaled. RCOND =  2.899200e-18.'
norm(A*x-b,1)             % computed solution is useless (as expected)    
ans =
     4.344157433375132e+00
 
mp.Digits(34);
x = mp(A)\mp(b);          % 34-digits takes care of ill-conditioning
norm(A*x-b,1)
ans = 
    4.336808689942017736029811203479767e-18
  4. Special functions
    • The whole family of Bessel functions has been re-written from scratch to support arbitrary arguments, orders and to improve speed. Also we have added both Hankel functions.

      Be aware that Symbolic toolbox in MATLAB gives low-accuracy results in some cases:

      % Symbolic Math Toolbox - R2015a
>> digits(34);
>> z = 8-43*1i;
>> besseli(1,vpa(z))
ans =
-17.2937_918159785... + 178.7197_1803657...i  % only 6-7 digits are correct!! 
 
% Advanpix Multiprecision Toolbox - 3.9.0.9919
>> mp.Digits(34);
>> besseli(1,mp(z))
ans = 
-17.29378620503294288287975364153844 + 178.7197375141310577798644760813918i % full accuracy
 
Maple:       -17.29378620503294288287975364153844 + 178.7197375141310577798644760813918*I
Mathematica: -17.29378620503294288287975364153844 + 178.7197375141310577798644760813918*I
 
% One more example:
>> bessely(0,vpa(1000*i))
ans =
-2.54099907...376797872e381 + 2.485686096075864174562771484145676e432i  % huge real part?
 
>> bessely(0,mp(1000*i))
ans = 
-1.28057169...387105221e-436 + 2.485686096075864174562771484145677e+432i % not really

      Now Advanpix toolbox is the only way to compute Bessel functions accurately and with high accuracy in MATLAB world.

    • Gamma and hypergeometric functions have been updated for accuracy, performance and stability. As usual, we are way faster that MATLAB itself:
      % Symbolic Math Toolbox - R2015a
>> digits(34);
>> z = 150*vpa((rand(50)-0.5)+(rand(50)-0.5)*1i);
>> tic; hypergeom([],vpa(1000-1000*i),z); toc;
Elapsed time is 6.208366 seconds.
 
>> tic; besseli(0,z); toc;
Elapsed time is 8.635691 seconds.
>> tic; besselk(0,z); toc;
Elapsed time is 9.938277 seconds.
>> tic; bessely(0,z); toc;
Elapsed time is 17.444061 seconds.
>> tic; besselj(0,z); toc;
Elapsed time is 10.570827 seconds.
 
% Advanpix Multiprecision Toolbox - 3.9.0.9919
>> mp.Digits(34);
>> Z = sym2mp(z);
>> tic; hypergeom([],mp('1000-1000*i'),Z); toc;
Elapsed time is 0.155974 seconds.      % x40 times faster
 
>> tic; besseli(0,Z); toc;
Elapsed time is 2.131102 seconds.      % x4 times faster
>> tic; besselk(0,Z); toc;
Elapsed time is 2.163481 seconds.      % x4.6 times faster
>> tic; bessely(0,Z); toc;
Elapsed time is 4.301771 seconds.      % x4 times faster 
>> tic; besselj(0,Z); toc;
Elapsed time is 3.228625 seconds.      % x3 times faster

      Also we have added the Lambert W function (only real arguments are supported for now).

  5. Formatted output.
    • The *printf functions now support matrix inputs and various whistles and bells for compatibility with built-in MATLAB functions (some weird exceptions as for integer format specifiers, etc.).
    • Added support for MATLAB’s line spacing setting (format compact/loose):
      >> mp.Digits(34)
>> mp.FollowMatlabNumericFormat(true);
 
>> A = mp(rand(2));
>> format loose
>> A
 
A = 
 
        0.4853756487228412241918817926489282        0.1418863386272153359612957501667552    
        0.8002804688888001116708892368478701        0.4217612826262749914363325842714403    
 
>> format compact
>> A
A = 
        0.4853756487228412241918817926489282        0.1418863386272153359612957501667552    
        0.8002804688888001116708892368478701        0.4217612826262749914363325842714403
 
>> format longE
>> A
A = 
        4.8537564872284122419188179264892824e-01      1.4188633862721533596129575016675517e-01    
        8.0028046888880011167088923684787005e-01      4.2176128262627499143633258427144028e-01
 
>> format shortE
>> A
A = 
        4.8538e-01        1.4189e-01    
        8.0028e-01        4.2176e-01
  6. Added/updated functions: besselh, lambertw, gradient, linspace, logspace, meshgrid, ndgrid, diff and isinteger.
  7. Miscellaneous small improvements and bug fixes for stability and speed.

As a side project, we have analysed and compared some common methods for computing the modified Bessel functions and proposed the improved minimax rational approximations: I0(x) and I1(x).

Acknowledgements

As always, our work on this release was influenced by feedback, bug reports and feature requests from many people. Thank you all for helping us improve the toolbox!

I am grateful to Prof. Edward J. Kansa for introduction of the RBF methods and for mentioning the toolbox in his keynote speech at the 2015 International Conference on Boundary Elements where he was awarded George Green medal for his fundamental contribution to meshless methods. Sincere congratulations!

Also I would like to thank Anne Russon who helped us to get access to the report[3] – as it is not available on Internet and Anne helped us to get the copy from archive of Canadian Nuclear Laboratories. Thank you Eleanor Miller and Tanya Martin!

References

  1. Kågström B., Kreßner D., Quintana-Ortí ES., Quintana-Orti G., Blocked algorithms for the reduction to Hessenberg-triangular form revisited, BIT Numerical Mathematics, 2008.^
  2. Kågström B., Kreßner D., Multishift variants of the QZ algorithm with aggressive early deflation, SIAM Journal on Matrix Analysis and Applications, 2006.
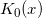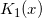  3. Russon A.E., Blair J.M., Rational function minimax approximations for the modified Bessel functions K_0(x) and K_1(x), AECL-3461, Chalk River Nuclear Laboratories, Chalk River, Ontario, October 1969.
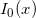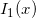  4. Blair J.M., Edwards C.A., Stable rational minimax approximations to the modified Bessel functions I_0(x) and I_1(x), AECL-4928, Chalk River Nuclear Laboratories, Chalk River, Ontario, October 1974.

{ 0 comments… add one now }

Leave a Comment

Previous post:

Next post: