Dear readers of the Advanpix blog,

My name is Denys Dutykh, a guest blogger today, and I would like to share my experience with the Multiprecision toolbox.

My research interests lie in the fields of applied mathematics and hydrodynamics. More precisely, with my collaborators we study mathematically free surface flows or, in other words, water waves.

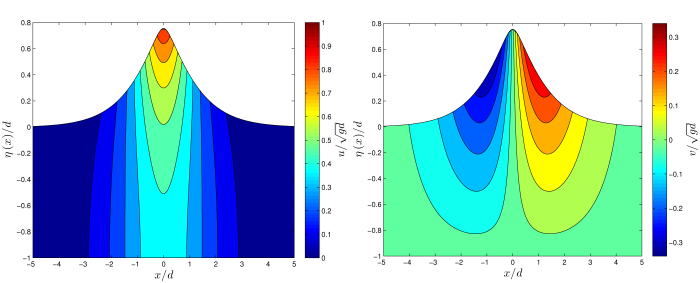
Solitary waves (i.e. localized structures travelling on the free surface) constitute a very important class of solutions. Recently in collaboration with Prof. Didier Clamond (LJAD, University of Nice Sophia Antipolis), we proposed a novel fast and accurate algorithm to compute these special solutions to the free-surface Euler equations. The method is based on conformal maps technique and the Petviashvili-type iteration. Moreover, this formulation allows to reconstruct all the fields of interest such as the potential, stream function, pressure, velocity, and acceleration in the bulk of the fluid. For the sake of illustration, we show the distribution of the horizontal and vertical velocities under a high amplitude solitary wave:

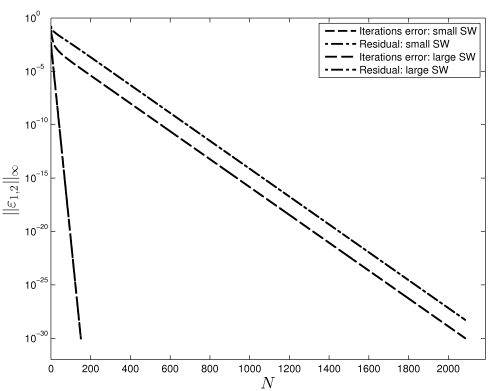
Even if in most practical situations the double precision arithmetic is sufficient, we were happy to perform some multiple precision computations to check the convergence and accuracy of the algorithm beyond the standard floating point arithmetic. Convergence of iterations for two different solitary wave amplitudes are shown below, where we used 33 digits in the mantissa.

Porting to the extended precision was quite straightforward thanks to the one-to-one compatibility of Advanpix Multiprecision Toolbox with MATLAB and rich set of functions it provides. Nevertheless, I can send the multi-precision version under a simple request. Double precision version of the script can be freely downloaded from the MATLAB Central File Exchange server: Solitary water wave.

For more information, you can have a look at the corresponding preprints currently submitted to peer-review journals:

• D. Clamond, D. Dutykh. Fast accurate computation of the fully nonlinear solitary surface gravity waves. Submitted, 2013.
• D. Dutykh, D. Clamond. Efficient computation of steady solitary gravity waves. Submitted, 2013.

Any questions, comments and remarks are welcome!

Dr. Denys Dutykh,
Guest blogger & Researcher @ CNRS (France) / UCD (Ireland)
http://www.denys-dutykh.com/