Rounding and cancellation errors are major sources of accuracy loss in numerical computing. To detect these effects researchers have to conduct rigorous analysis of every operation in the algorithm both on the theoretical and computational level.
Multiprecision Computing Toolbox allows users to save time by applying a simple procedure to detect accuracy loss in their MATLAB programs. Using the toolbox researcher is able to re-run computations in elevated precision – with little or no modifications to existing source code.
If the results change significantly with increase of precision, chances are there is numerical instability somewhere in the computations. Otherwise computations are stable and time consuming analysis can be safely skipped.
Accuracy verification is one of the classic applications of the toolbox. As an illustration, we will share an example provided by one of the toolbox users who was able to detect and overcome a cancellation error in his computations using the toolbox.
Example
Our task is to find zeros of the following function:
![]()
Standard MATLAB function fzero solves this easily for any ![]() :
:
f = @(x) sin(x).^2+cos(x).^2+2*cos(x).*cosh(x)+cosh(x).^2-sinh(x).^2; x = fzero(f, 5) x = 4.69409113297418 x = fzero(f, 10) x = 10.9955407348782 x = fzero(f, 15) x = 14.1371683911517 ... x = fzero(f, 30) x = 29.8449784514733
However for higher values of ![]() ,
, fzero demonstrates strange behavior by returning the starting point itself:
>> x = fzero(f, 40) x = 40 >> x = fzero(f, 50) x = 50 >> x = fzero(f, 60) x = 60 ... >> x = fzero(f, 100) x = 100
In spite of obvious “problem”, MATLAB’s diagnostics insures us of normal zero-search termination:
>> [x,feval,flag] = fzero(f, 50) x = 50 feval = 0 flag = 1
Here is plot of the function produced by MATLAB:
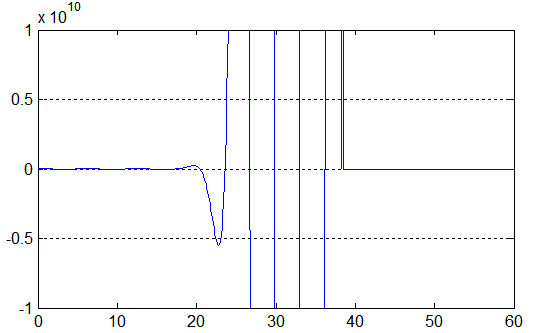
Very strange indeed! MATLAB shows the function as a zero-constant in the upper half of interval which doesn’t make any sense.
Explanation
The reason of such abnormality is in the limited accuracy of computations in MATLAB. The function consists of two approximately equal parts which are subtracted from each other:
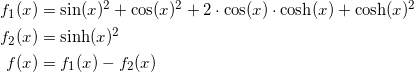
Both sub-functions quickly grow by magnitude for ![]() . Let’s see how MATLAB computes them for big
. Let’s see how MATLAB computes them for big ![]() .
.
f1 = @(x) sin(x).^2+cos(x).^2+2*cos(x).*cosh(x)+cosh(x).^2; f2 = @(x) sinh(x).^2; >> x0 = 41 >> a = f1(x0) a = 1.02349924053186e+035 >> b = f2(x0) b = 1.02349924053186e+035 >> a-b ans = 0
Compare this with high precision results produced by the toolbox:
>> mp.Digits(50); >> a = f1(mp(x0)) 102349924053186366784780243102910145.20763037783874 >> b = f2(mp(x0)) 102349924053186367416522855733195725.58001344804846 >> a-b -631742612630285580.3723830702097248042772067305739
As we see "a" and "b" differ starting from the 17-18th decimal place.
However, MATLAB is able to store only about 16 decimal places of a number. All places beyond this limit are ignored (wiped out). As a result, MATLAB treats both numbers as “equal”, giving a zero in subtraction in spite of their original non-equality.
In general when two numbers are nearly equal (comparable by magnitude) there is a risk of such “cancellation” error in subtraction.
Overcoming Cancellation Error
To detect and overcome the cancellation error, one needs to use extended precision arithmetic to repeat computations with extended accuracy. If the results do not change significantly with change of precision this will indicate stable computations.
For example, if we repeat finding zeroes using 50 places accurate arithmetic, we will get the following results:
>> mp.Digits(50); >> x = fzero(f, mp('40')) 39.269908169872415498416016514292083430031798260673 >> x = fzero(f, mp('50')) 48.694686130641795196169549468319144925821315530214 >> x = fzero(f, mp('60')) 61.261056745000968150021545968986661796101537482934
Precise plot of the function can also be computed using the toolbox:
x = mp(0):mp('.1'):mp('60'); y = f(x); plot(x,y) axis([0 60 -1e+10 1e+10]);
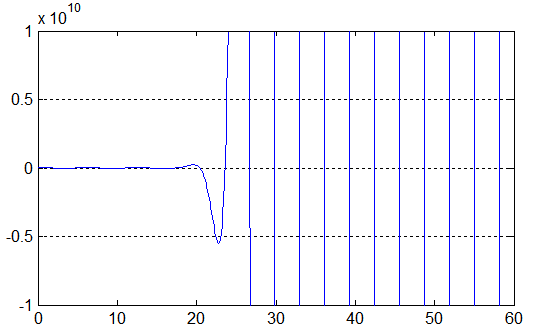

{ 0 comments… add one now }